Eulerian motion
Description:
When the rocket flies, it is acted upon by the Euler motion, which changes the angular velocity and rotates the rocket. You need to calculate how it's changes. For do this we have the dynamic Euler equation

and kinetic Euler equation
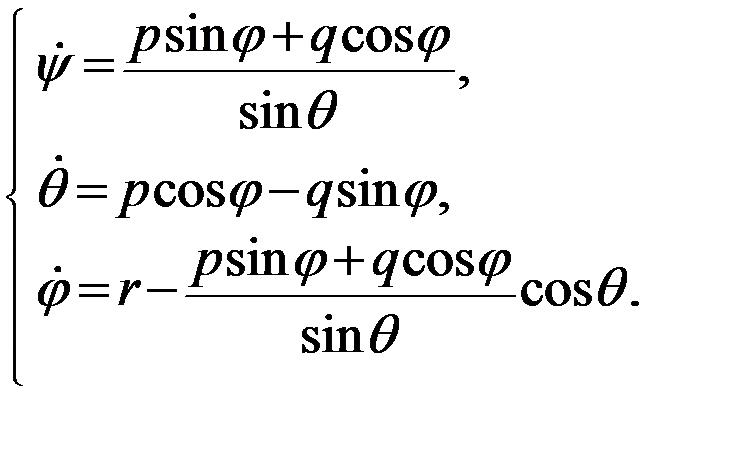
And we got a start position: vector<double> Position={P0,Q0,R0,Fi0,Teta0,Psi0}.
You need to integrate this systems at start position by Runge-Kutta 4th order

to have next position at setting step h.
Input data:
A, B, C, Gx, Gy, Gz, h and vector<double> Position={P0,Q0,R0,Fi0,Teta0,Psi0};
Output data:
vector<double> Result={P1,Q1,R1,Fi1,Teta1,Psi1};
Mark: Fi, Teta, Psi are given in degrees. You must convert to radians M_PI/180 to make the calculation and in answer return to degree. And 0<=Fi<360, if Fi<0 or Fi>=360 you must +360 or -360 until Fi get to the range, the same is Teta and Psi. And the values are rounded to 3 decimal places
Similar Kata:
Stats:
| Created | Apr 6, 2018 |
| Published | Apr 6, 2018 |
| Warriors Trained | 163 |
| Total Skips | 32 |
| Total Code Submissions | 21 |
| Total Times Completed | 6 |
| C++ Completions | 6 |
| Total Stars | 4 |
| % of votes with a positive feedback rating | 33% of 3 |
| Total "Very Satisfied" Votes | 1 |
| Total "Somewhat Satisfied" Votes | 0 |
| Total "Not Satisfied" Votes | 2 |
| Total Rank Assessments | 2 |
| Average Assessed Rank | 6 kyu |
| Highest Assessed Rank | 5 kyu |
| Lowest Assessed Rank | 6 kyu |